[통계 1]모집단과 표본, 분산과 표준편차

1. 모집단과 표본

 

통계를 통해 사회현상을 분석할 때, 모집단과 표본이라는 말을 먼저 알아야 한다.

예를 들어 전국의 중학생 수가 100만이라고 할 때, 전국 중학생들의 학업 성취도 조사를 한다고 해보자.

100만을 모두 뽑아서 조사하기에는 한계가 있기 때문에 그 중 일부를 뽑아 조사하는데 그 것이 바로 표본(sample)이고 전체 100만 학생을 모집단(population)이라고 한다.

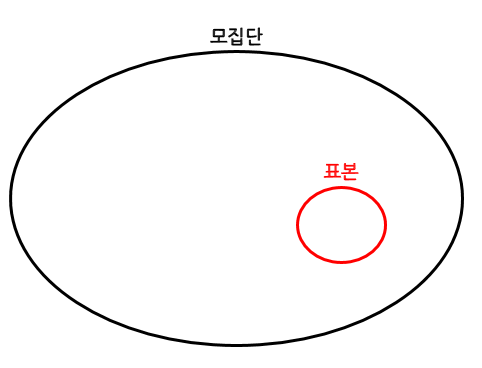
표본에 대해서도 평균,표준편차, 분산과 같이 통계적 수치가 있고 다음과 같이 표현한다.

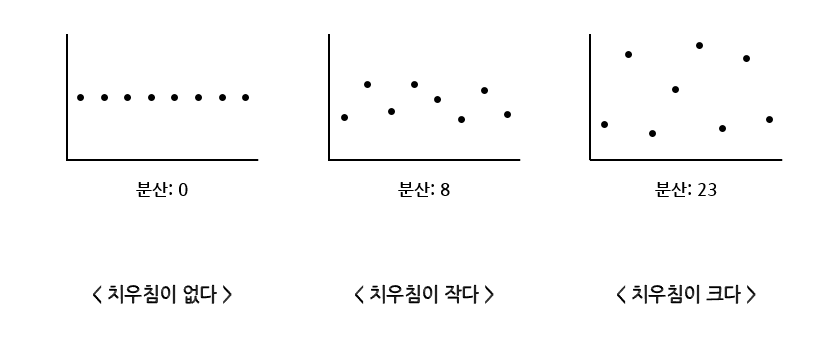
여기서 말하는 분산은 말 그대로 분산의 정도, 흩어짐의 정도를 말한다고 보면 된다.

모든 데이터가 평균 값을 가지면, 분산값은 0이고, 평균 값과 많이 멀리 있는 데이터가 많을 수록 분산 값이 크다고 볼 수 있다.

분산은 표준편차의 제곱으로 표현된다.

 

 

분산을 구하는 공식은 다음과 같다.

모집단의 분산을 모분산,표본집단의 분산을 표본집단으로 표현하는데, 표본분산은 모분산과 다르게 n-1로 나눈다.

표본분산의 값을 구할 때, n-1로 나누는 이유는 모분산의 값과 유사하기 때문이다.